The relationship between Voltage, Current and Resistance in a Direct Current electrical circuit was first discovered by the German physicist and mathematician Georg Ohm. Publishing his work in 1827, he found that, at a constant temperature, the electrical current flowing through a fixed linear resistance is directly proportional to the voltage applied across it, and also inversely proportional to the resistance. This relationship between the Voltage, Current and Resistance forms the basis of Ohm’s Law and is shown below.

Ohm’s Law Relationship

By knowing any two values of the Voltage, Current or Resistance quantities, we can use Ohm’s Law to find the third missing value. Ohm’s Law is used extensively in electrical and electronic designs and calculations.

Conventions:

V= Potential difference, known as Voltage, is measured as a number of Volts (V), named after Alessandro Volta.
I= Electrical current intensity (I) is measured as a number of Amperes (sometimes shortened to ‘Amps’) (A), named after André-Marie Ampère.
R= Resistance is measured as a number of Ohms (Ω), named after Georg Ohm.

To find the Voltage, (V)
[ V = I x R ]      V (volts) = I (amps) x R (ohms)
To find the Current, (I)
[ I = V ÷ R ]      I (amps) = V (volts) ÷ R (ohms)
To find the Resistance, (R)
[ R = V ÷ I ]      R (ohms) = V (volts) ÷ I (amps)

It is sometimes easier to remember this Ohm’s law relationship by using pictures. Here the three quantities of V, I and R have been superimposed into a triangle giving voltage at the top with current and resistance below. This arrangement represents the actual position of each quantity within the Ohm’s law formulas.

Ohm’s Law Triangle

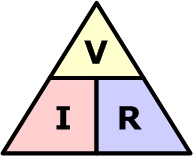
Transposing the above Ohm’s Law equation gives us the following combinations of the same triangle:

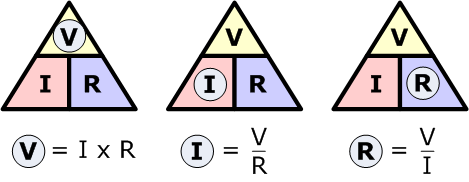
By using Ohm’s Law we can see that a voltage of 1 Volt applied to a resistor of 1 Ohm will cause a current of 1 Amp to flow and the greater the resistance value, the less current that will flow for a given applied voltage.