Electrical Power

The electric power (in watts) associated with a complete electric circuit or a circuit component represents the rate at which energy is converted from the electrical energy of the moving charges to some other form, e.g., heat, mechanical energy, or energy stored in electric fields or magnetic fields.

For a resistor in a Direct Current (DC) circuit the power is given by the product of applied voltage and the electric current:

Electrical Power in Circuits

Power (P) in a circuit is the amount of energy that is absorbed or produced within the circuit. A source of energy such as a voltage will produce or deliver power while the connected load absorbs it. Light bulbs and heaters for example, absorb electrical power and convert it into heat or light. The higher their value or rating in watts the more power they will consume.

The quantity symbol for power is P and is the product of voltage multiplied by the current with the unit of measurement being the Watt (W).

Prefixes are used to denote the various multiples or sub-multiples of a watt, such as: milliwatts (mW = 10^-3W) or kilowatts (kW = 10³W).

Then by using Ohm’s law and substituting for the values of V, I and R the formula for electrical power can be found as:

To find the Power (P)

Also,

Also,

As with the Ohm's law equation, the three quantities can be superimposed into a triangle this time called the Power Triangle with power at the top and current and voltage at the bottom. Again, this arrangement represents the actual position of each quantity within the power formulas.

The Power Triangle

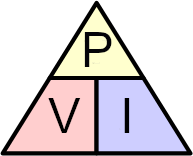
and again, transposing the basic Ohms Law equation above for power gives us the following combinations of the same equation to find the various individual quantities:

P=VxI

I=P/V

V=P/I

So we can see that there are three possible formulas for calculating electrical power in a circuit. If the calculated power is positive in value for any formula the component absorbs the power, that is it is consuming or using power. But if the calculated power is negative in value the component produces or generates power, in other words it is a source of electrical power such as batteries and generators.

Electrical Power Rating

Electrical components are given a “power rating” in watts that indicates the maximum rate at which the component converts the electrical power into other forms of energy such as heat, light or motion. For example, a 1/4W resistor, a 60W light bulb etc.

Electrical devices convert one form of power into another. So for example, an electrical motor will covert electrical energy into a mechanical force, while an electrical generator converts mechanical force into electrical energy. A light bulb converts electrical energy into both light and heat.

So, we now know that the unit of power is the Watt, but some electrical devices such as electric motors have a power rating in the old measurement of “Horsepower” (hp). The relationship between horsepower and watts is given as: 1hp = 746W. So for example, a two-horsepower motor has a rating of 1492W, (2 x 746) or 1.5kW.

Ohms Law

To help us understand the the relationship between the various values a little further, we can take all of the equations for finding Voltage, Current, Resistance and Power and use them to calculate values in a circuit.

A circuit has the following values:

Voltage = 24 volts, Current = 2 amps, resistance = 12 ohms, Power = 48 watts

But how did we calculate these values?

Here is how we found the Voltage (V), the Current (I), the Resistance (R) and the Power (P).

Voltage [ V = I x R ] = 2 x 12 = 24 volts

Current [ I = V ÷ R ] = 24 ÷ 12 = 2 amps

Resistance [ R = V ÷ I ] = 24 ÷ 2 = 12 ohms

Power [ P = V x I ] = 24 x 2 = 48 watts

Power within an electrical circuit is only present when BOTH voltage and current are present.

For example, in an open-circuit condition, voltage is present but there is no current flow I = 0 (zero), therefore >V x 0 is 0 so the power dissipated within the circuit must also be 0.

Likewise, if we have a short-circuit condition, current flow is present but there is no voltage V = 0, therefore >0 x I = 0 so again the power dissipated within the circuit is 0.

As electrical power is the product of V x I, the power dissipated in a circuit is the same whether the circuit contains high voltage and low current or low voltage and high current flow (although your circuit components will disagree).

Generally, electrical power is dissipated in the form of Heat (heaters), Mechanical Work such as motors, Energy in the form of radiated energy (Lamps) or as stored energy (Batteries).

Electrical Energy in Circuits

Electrical Energy is the capacity to do work, and the unit of work or energy is the joule ( J ). Electrical energy is the product of power multiplied by the length of time it was consumed. So if we know how much power, in Watts is being consumed and the time, in seconds for which it is used, we can find the total energy used in watt-seconds. In other words, Energy = power x time and Power = voltage x current. Therefore electrical power is related to energy and the unit given for electrical energy is the watt-seconds or joules.

Electrical power can also be defined as the rate of by which energy is transferred. If one joule of work is either absorbed or delivered at a constant rate of one second, then the corresponding power will be equivalent to one watt so power can be defined as “1Joule/sec = 1Watt”. Then we can say that one watt is equal to one joule per second and electrical power can be defined as the rate of doing work or the transferring of energy.

Although electrical energy is defined as being watts per second or joules, electrical energy measured in Joules can often become a very large value when used to calculate the energy consumed by a component.

For example, if a 100 watt light bulb is left  energised (“ON”) for 24 hours, the energy consumed will be 8,640,000 Joules (100W x 86,400 seconds), so prefixes such as kilojoules (kJ = 10³J) or megajoules (MJ = 10⁶J) are used instead and in this simple example, the energy consumed will be 8.64MJ (mega-joules).

But dealing with joules, kilojoules or megajoules to express electrical energy, the maths involved can end up with some big numbers and lots of zero’s, so it is much more easier to express electrical energy consumed in Kilowatt-hours.

If the electrical power consumed (or generated) is measured in watts or kilowatts (thousands of watts) and the time is measure in hours not seconds, then the unit of electrical energy will be the kilowatt-hour,(kWhr). Then our 100 watt light bulb above will consume 2,400 watt hours or 2.4kWhr, which is much easier to understand than 8,640,000 joules.

1 kWhr is the amount of electricity used by a device rated at 1000 watts in one hour and is commonly called a “Unit of Electricity”. A Unit of Electricity (KiloWatt Hour) is what is measured by an electricity utility meter and is what we as consumers purchase from our electricity suppliers when we receive our bills.

Kilowatt-hours are the standard units of energy used by the electricity meter in our homes to calculate the amount of electrical energy we use and therefore how much we pay. So if you switch ON an electric fire with a heating element rated at 1000 watts and left it on for 1 hour you will have consumed 1 kWhr of electricity. If you switched on two electric fires each with 1000 watt elements for half an hour the total consumption would be exactly the same amount of electricity – 1kWhr.

So, consuming 1000 watts for one hour uses the same amount of power as 2000 watts (twice as much) for half an hour (half the time).

Theerfore for a 100 watt light bulb to use 1 kWhr or one unit of electrical energy it would need to be switched on for a total of 10 hours (10 x 100 = 1000 = 1kWhr).